Merge sort is a sorting algorithm with a simple strategy: divide and conquer. Here's a quick tutorial with examples of how to implement top-down and bottom-up methods in Swift.
The steps for merge sort are simple:
- Split the unsorted array containing N elements into N arrays containing one element each
- Merge the piles together by sequentially pairing piles together in sorted order
Here is an image explaining how this works:

Top-Down vs Bottom-Up
A top-down merge sort splits the array into smaller pieces and then merges them. This works, but because we're using an Array we can skip the first step (splitting) and start merging the elements immediately. That implementation is called bottom-up. Below you'll find examples of both methods.
Top-Down Implementation
Here's an example of a top-down implementation of merge sort in Swift:
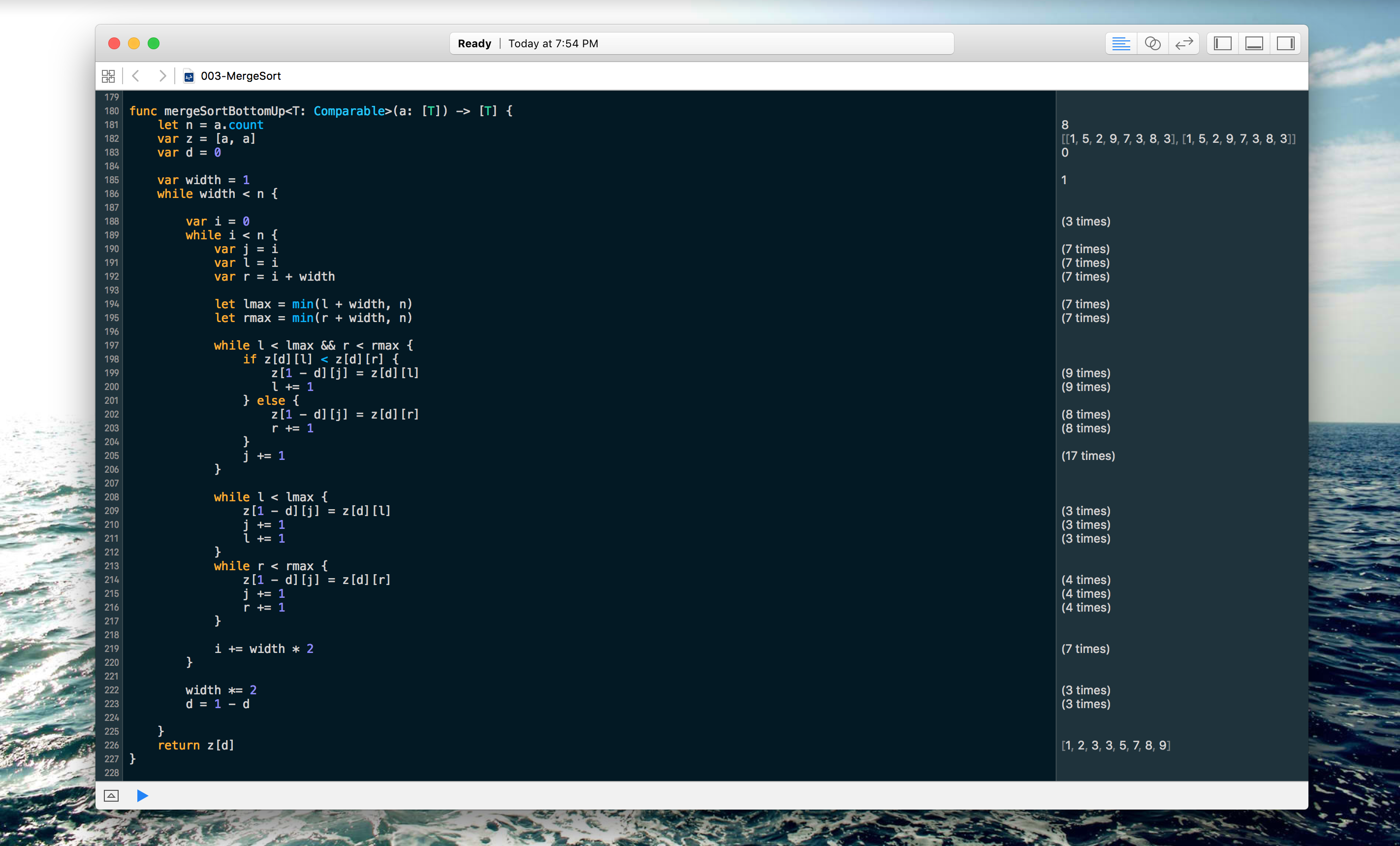
Bottom-Up Implementation
Here's an example of a bottom-up implementation of merge sort in Swift. Note this also uses Swift Generics, and will work with non-Int objects.
And one with an insane amount of comments and debug logging, because that's how I prefer to dive in to new algorithms to understand their inner-workings:
A Note on Double Buffering
If you take a look at the bottom-up implementation, you'll notice we need to allocate two arrays: one for reading and one for writing. This is called double buffering, and is necessary because you can't merge the array while changing its items.
In the bottom-up example above, you'll notice we're swapping out the "read" and "write" arrays. This is because every pass we make that modifies the "write" array will give us a new starting point. On every new pass, we're using the old "write" array as the new "read". When the width we're examining is equal to the array size, we know we're finished.
Memory Use
One of the disadvantages of using merge sort is the need to copy the array into a temporary array for sorting. If you're working in a memory-constrained environment, keep in mind you'll need 2N memory, where N is the size of the original array.
If you can't spare the memory, it might make sense to use insertion sort or selection sort, as they can sort in-place.
When To Use Merge Sort
The time complexity for the best, worst, and average cases with merge sort will be O(n_log_n).
If you're working in a memory-constrained environment, you may want to use an in-place sorting algorithm like insertion sort, which is a bit slower with an average performance of O(n^2) and best case performance of O(n).
References
If you have any questions, comments, or concerns, let me know!.